Chaotic Dynamical Systems

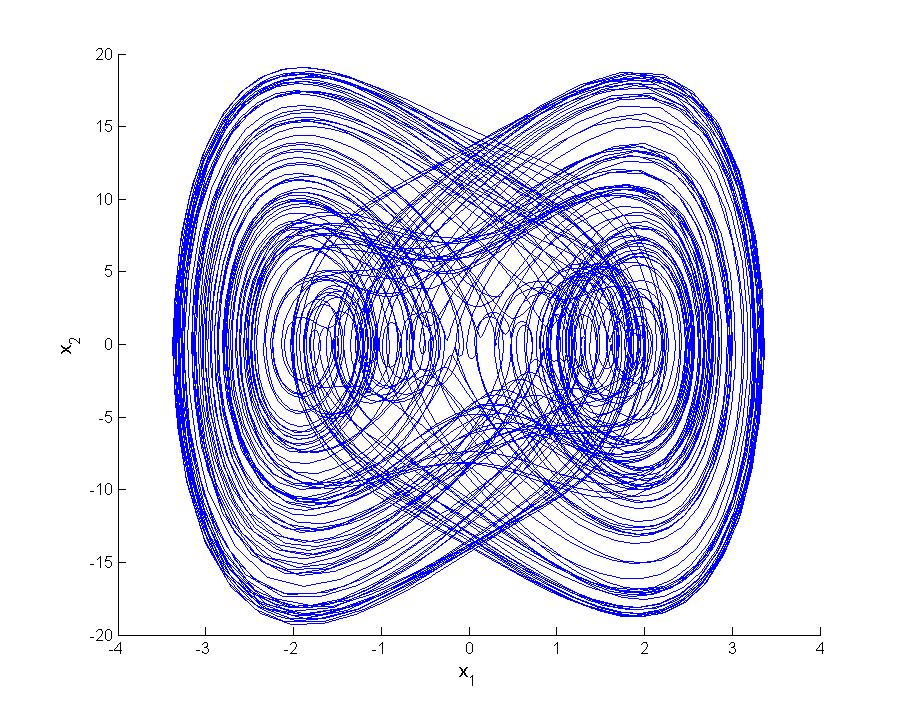
The studies on chaotic dynamics may be said to have started with the work of H. Poincaré about the problem of the orbits of three celestial bodies. Subsequent mathematical studies about chaos theory are done by G. Birkhoff in the 1920s, M. L. Cartwright and Littlewood in 1940s and S. Smale in 1960s. In the literature, ingredients of chaos such as sensitive dependence on initial conditions, transitivity and density of periodic solutions are mostly investigated as “endogeneous” properties of dynamical systems. The chaotic systems of Lorenz, Rössler and Duffing oscillators are some examples for endogeneously generated chaos. Our main attension is about extension of chaotic behavior in systems with arbitrary high dimensions. We propose by means of “chaotic” forcing terms to chaotify systems which are initially non-chaotic, for example, systems which possess stable equilibriums or orbitally stable limit cycles. In other words, by the proposed method one can achieve chaotic ingrediens as “exogeneous” properties. Chaos in the sense of Devaney and Li-Yorke and obtained through period-doubling cascade constitute the essential parts of our theoretical researches and studies.