Impulsive Differential Equations

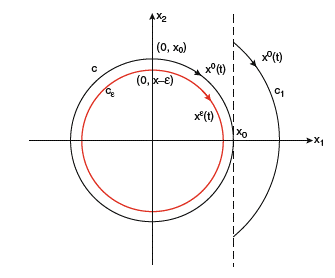Many mathematicians agree that discontinuity as well as continuity should be considered when one seeks to describe the real world more adequately.Real world problems are generally distract with an impact coming from outside that is why modelling in impulsive differantial equation is a convenient tool to understand the problem.It gives more rigorous results to analyze our problems. Impulsive differential equations seem appropriate for modeling motions where continuous changes are mixed with impact type changes in equal proportion.Impulsive differantial equations are convenient in modelling in mechanics, electronics, biology, neural networks, medicine, and social sciences.